Teorema
de Pitágoras
El
teorema de Pitágoras nos establece que en todo los triángulos rectángulos, el
cuadrado del lado de mayor longitud de algún triangulo rectángulo, (el cuadrado
de la hipotenusa) es igual a la suma de los cuadrados de los catetos (que son
los dos lados menores del triángulo los que conforman el ángulo recto).
El área del cuadrado que está
construido, dibujado, o que se encuentra sobre la hipotenusa del triángulo
rectángulo, es exactamente igual a la suma de las áreas de los cuadrados que se
encuentran construidos sobre los catetos.
Si en vez de construir un cuadrado en los lados de un triángulo
rectángulo, construimos cualquier otra figura, no cambia nada, el área de la
figura construida sobre la hipotenusa, sigue siendo la misma que la suma de las
áreas de las figuras que se encuentran construidas sobre los catetos.
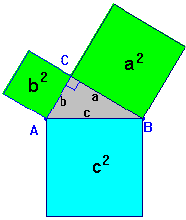
Una de las demostraciones geométricas es:
Pitágoras: a partir de la
igualdad de los triángulos rectángulos es evidente la igualdad: a2 + b2 = c2
Demostración algebraica: dependiendo o valiéndose de la construcción
que se es representado en cada caso, se han dado a lo largo de la historia
excelentes o muy buenas y sobre todo originales demostraciones.
Estas son algunas de las más populares:
Leonardo da vinci
Garfield

vieta .
Algunos autores, nos hablan de la existencia de hasta 1000 diferentes
demostraciones del teorema de Pitágoras.
Descubrimos, las personas que no sabíamos, que los sellos postales
rinden homenaje a Pitágoras y a su teorema:












No hay comentarios.:
Publicar un comentario